Le schéma général

La stratégie de dénonciation mutuelle permettrait, pour chacun, un gain moindre (1,1) que la stratégie de coopération (3,3)

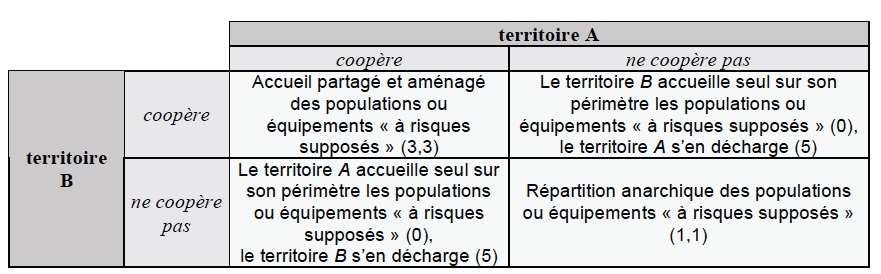
L’accueil des réfugiés, vu par la théorie des jeux (Tableaux de Bussi et Daudé, 2005)

Définition des principaux concepts

En mathématiques appliquées à l’Économie, la théorie des jeux modélise des situations conflictuelles où les individus peuvent coordonner leurs décisions. Selon R. Axelrod (1984), c’est un modèle donnant-donnant : ce qui est optimal dépend des anticipations sur le comportement des autres (voir le dilemme du prisonnier).

Il n’y a pas de véritable « solution » au sens mathématique, mais on représente en général les déroulements possibles d’un jeu par une matrice ou un arbre des gains. Suivant les issues possibles et leurs probabilités, il existe alors des algorithmes pour déterminer le « meilleur choix ». Pour modéliser certaines situations, un joueur non stratégique, la Nature, peut même prendre aléatoirement certaines décisions à telle ou telle étape du jeu : cela ne fait qu’orienter la suite du jeu vers un sous-arbre de l’arbre du jeu.

1. La classe de jeux coopératifs relevant du « dilemme du prisonnier »

Cette classe de jeux, décrite par Tucker (voir Eber 2006, voir Petit 2013) est emblématique des jeux coopératifs (les engagements sont irrévocables et garantis par une institution implicite) à somme non nulle (les deux joueurs peuvent perdre) et avec un nombre fini de stratégies  (deux stratégies dans le dilemme du prisonnier : avouer ou ne pas avouer).

Bien que chaque malfaiteur ait personnellement intérêt à avouer, l’intérêt commun est de ne pas avouer (c’est la stratégie de coopération), en effet les choix sont toujours simultanés et on voit sur le schéma ci-dessus que:

• si un seul avoue, il est relaxé (son gain est estimé à 5) mais son complice écope la peine maximum de dix ans de prison (son gain est estimé à 0);
• si les deux avouent, ils sont condamnés tous les deux à cinq ans de prison (leurs gains sont estimés à 1 et 1);
• mais si aucun n’avoue, alors la seule charge retenue contre eux deux est le port d’arme et la condamnation est réduite à deux ans de sursis pour chacun (équilibre qui nécessite la coopération, et leurs gains sont estimés à 3 et 3).

“Résoudre” le dilemme du prisonnier consiste à rendre stable cette stratégie de coopération qui consiste à ne jamais avouer alors qu’on ne « sait » pas encore ce que l’autre va faire. (voir cette animation vidéo issue d’un MOOC de l’UCL). Mais dans la réalité, comment faire des anticipations rationnelles sur le comportement subjectif de l’autre : en fonction d’une confiance répétée? de la réputation des joueurs? du coût d’une trahison? d’une convention? Or toute la théorie des jeux se fonde sur des fonctions de préférences qui doivent être continues et sur des stratégies qui doivent être probabilistes et non pas aléatoires (sur les hypothèses de la théorie des jeux, voir Walliser 2002).

2. A la recherche d’un « équilibre de Nash »

Un équilibre de Nash (voir Brasseur 2005) est une situation stable  où chacun anticipe correctement ce que les autres vont faire, alors:

• aucun joueur n’a intérêt à dévier unilatéralement de sa stratégie (“toutes choses égales par ailleurs”);
• et aucun joueur ne regrette son choix après avoir constaté celui des autres joueurs : il n’aurait pas pu faire mieux et on a maximisé les gains nets.

Dans les jeux finis en stratégies mixtes (c’est à dire avec un nombre fini de stratégies, et que les joueurs choisissent de manière probabiliste) J. Nash a démontré mathématiquement qu’il y a toujours au moins un équilibre stable (mais pas nécessairement optimal, ni nécessairement unique).

D’un point de vue méthodologique les décisions en interactions-coopérations sont souvent étudiées « en laboratoire », dans des situations expérimentales de jeux de gains et pertes probables. Cette méthodologie est aujourd’hui devenue le support principal de l’Économie comportementale pour analyser les décisions individuelles.

3. Les fonctions de préférences et les jeux non coopératifs

Dans la réalité, si nos “fonctions de préférences” existent, elles ne sont en tout cas pas continues : une modification infime d’une stratégie peut modifier radicalement notre bien-être et il n’y a donc pas vraiment de situations stables décrites par l’équilibre de Nash. Dans ce cas, Simon et Zame ont démontré que si l’on autorise la modification de la règle de partage des gains, il peut à nouveau exister des situations d’équilibre, mais alors au prix d’une hypothèse très forte pour la théorie des jeux car il faut alors autoriser les joueurs à adopter des stratégies aléatoires et non pas probabilistes (voir Bich et Laraki, 2014).

Une autre classe de jeux est celle des jeux non coopératifs, dans lesquels il peut exister plusieurs équilibres et donc avec des accords stratégiques qui sont auto-exécutables, c’est à dire non garantis par une institution. Il s’agit alors de prendre en compte les négociations sur le partage formel des gains (par exemple en négociant une règle du type « partage d’héritage ») et les négociations sur les procédures formelles permettant aux joueurs de mettre en œuvre la solution (par exemple des règles du type droit de veto, coalitions partielles, offres alternées…). Même si la multiplicité de ces procédures formelles négociées éloigne de l’idée d’une solution mathématique rigoureuse, la théorie des jeux non coopératifs est un « cadre pédagogique » formel pour éclairer des situations de négociations internationales ou de coalitions dans des réseaux d’entreprises (voir Péreau 2009).

En rendant finalement endogène l’action sur les règles et leur modification par des « arrangements » successifs (cheap talk dans des arènes locales de discussion), Elinor Ostrom abandonne alors la théorie des jeux, pour proposer le modèle du Choix institutionnel. Elle démontre que dans le cas du partage d’une ressource commune  (les biens communs), les systèmes de coopération du type « dilemme du prisonnier » (où ce sont des règles externes et exogènes qui organisent les comportements collectifs en fonction de l’intérêt personnel) sont en fait moins efficaces que les systèmes de coopération de type « dilemme social » (où la modification des règles se fait en interne par des arrangements successifs, en fonction de l’information partagée dans des « arènes locales » de discussion sur toutes les variables situationnelles).

.

Voir les autres théories utilisées dans le développement des SI

Voir la carte générale des théories en management des S.I.